Highly Available Transactions: Virtues and Limitations (2013)
January 30, 2025Overview
The CAP theorem’s trilemma of consistency, availability, and partition tolerance does not require sacrificing one property entirely but rather prioritizing among the three. Given a specific consistency model, how much availability is feasible? The paper Highly Available Transactions: Virtues and Limitations explores the relationship between consistency models and their achievable availability. It organizes each consistency-availability pair into a partial order based on their strengths.
Availability
The authors assume the presence of network partitions and associate two types of availability, high availability and sticky availability, with consistency models.
A system provides high availability if every user that can contact a correct (non-failing) server eventually receives a response from that server, even in the presence of arbitrary, indefinitely long network partitions between servers.
High availability states that every client that can contact a correct (non-failing) server eventually receives a response from that server, even in the presence of arbitrary, indefinitely long network partitions between servers. This definition originates from Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services.
Sticky availability states that whenever a client’s transactions is executed against a replica that reflects all of the client’s prior operations, it eventually receives a response, even in the presence of indefinitely long partitions.
Partial ordering of consistency
High availability and sticky availability can be ordered by their strength.
The systems that provide high availability also satisfy sticky availability, but not vice versa.
The following image, cited from the paper, illustrates the paritial order of the strength of consistency.
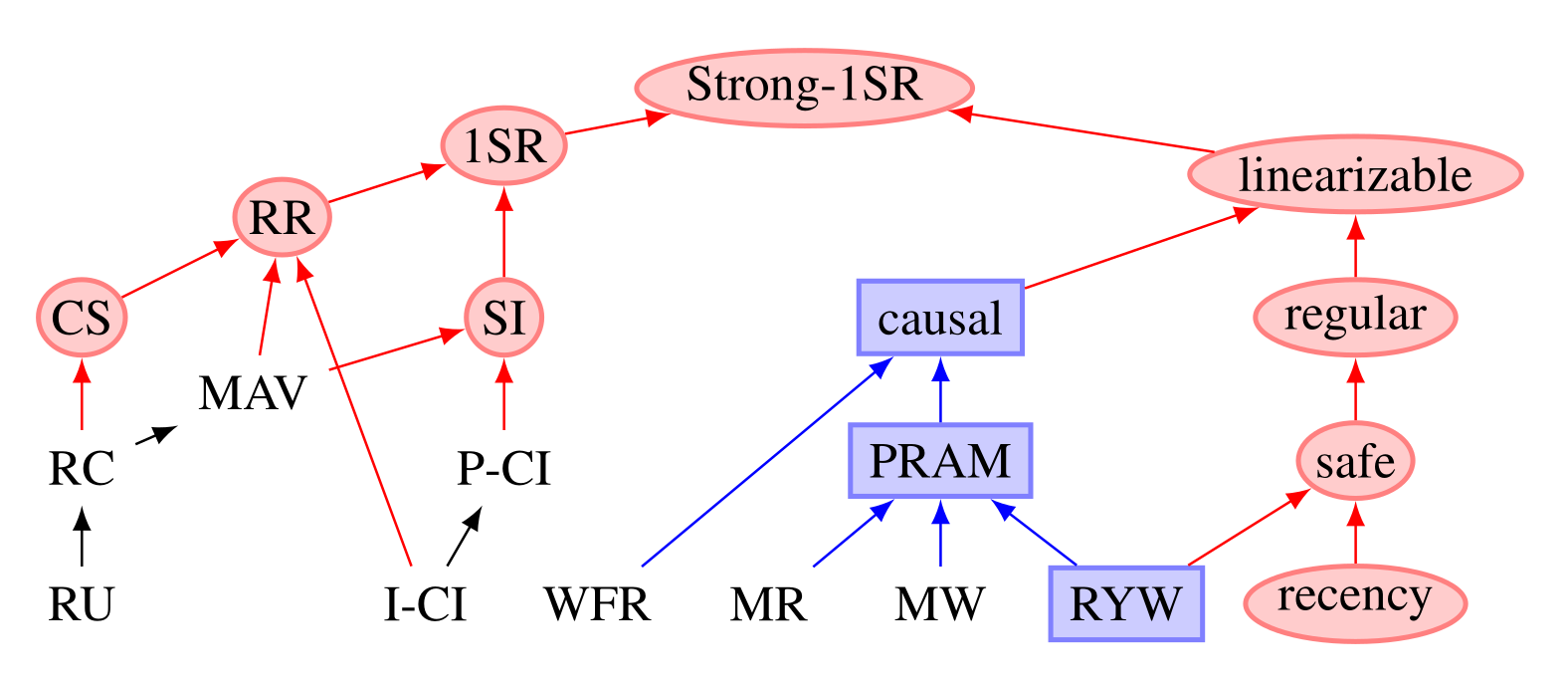
The nodes in the diagram represent consistency models. Nodes that are not enclosed indicate high availability. Rectangular nodes denote sticky availability, while oval nodes represent unattainable models. The higher a node appears, the stronger the consistency and the lower the availability it provides.
The figure and its explanation are also available on the Jepsen website, a fault injection framework for distributed systems. The explanation in the website is more informative than that of the paper. The paper references the original works that introduced these consistency models for detailed explanations.
In WFR (Writes Follow Reads), If a process commits transaction \(T_1\) followed by transaction \(T_2\), no other process can observe \(T_2\)’s result before \(T_1\)’s result. Causal consistency ensures that all processes agree on the order of causally related operations, though they may disagree on the order of causally independent operations. Linearizability guarantees that each operation applied by concurrent processes takes effect instantaneously at some point between its invocation and its response.