Improving Language Understanding by Generative Pre-Training (2018)
November 16, 2025 (Originally posted on August 7, 2020)Improving Language Understanding by Generative Pre-Training describes the original generative pre-trained transformer model. The paper shows that pre-training on unlabeled text followed by fine-tuning on supervised tasks leads to strong performance. During fine-tuning, the output of the pre-trained model is passed to a linear output layer.
The model described in the paper is based on a multi-layer Transformer decoder. Unlike the architecture in Attention Is All You Need, this model uses only the decoder stack. Representations for upstream tasks are constructed so that their format aligns with the unlabeled text used in pre-training. For example, an entailment example is created by concatenating the premise and the hypothesis with a delimiter. A text similarity task also concatenates two texts with a delimiter and feeds the sequence into the pre-trained model.
Given unlabeled tokens \(\mathcal{U}=\{u_1,\dots , u_n\}\), pre-training maximizes the likelihood:
$$ L\_1(\mathcal{U})=\sum\_i\log P(u\_i\mid u\_{i-k},\dots , u\_{i-1};\Theta), $$where \(k\) is the context window size, and \(P\) is the conditional probability modeled by the Transformer decoder with parameters \(\Theta\). Let \(U=(u_{-k}, \dots, u_{-1})\) be the input tokens, \(W_e\) the token embedding matrix, and \(W_p\) the position embedding matrix. The first Transformer block receives the sum of token and position embeddings:
$$ \begin{align} h_0&=UW_e+W\_p\\\\ h_l&=\mathtt{transformerblock}(h_{l-1})\forall i \in[1,n]\\\\ P(u)&=\texttt{softmax}(h\_nW^{T}\_{e}) \end{align} $$During fine-tuning, for an instance consisting of tokens \(x^1,\dots , x^m\) with label \(y\), a linear output layer reads the final hidden state \(h^m_l\) of the last token:
$$ \begin{align} P(y\mid x^1 , \dots , x^m) &= \texttt{softmax}(h^m\_lW\_y) \\\\\ L\_2(\mathcal{C})&=\sum\_{(x,y)}\log P(y\mid x^1\dots , x^m)\\\\\ \end{align} $$
The figure below illustrates the data representations used for upstream tasks.
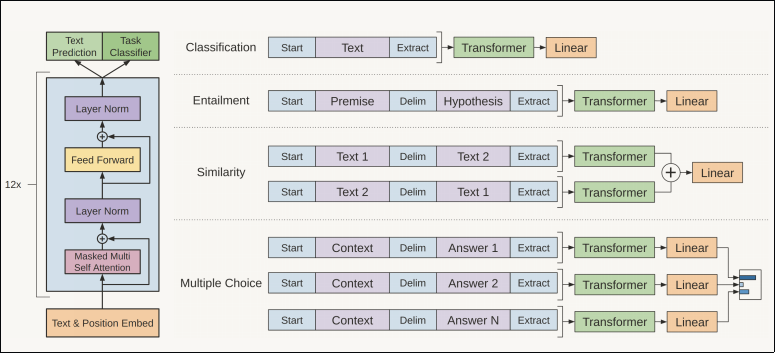
In addition to \(L_2(\mathcal{C})\), the paper also considers an auxiliary objective \(L_3(\mathcal{C})\) to improve generalization and accelerate convergence:
$$ L\_3(\mathcal{C})=L\_2(\mathcal{C})+\lambda * L\_1(\mathcal{C}) $$where \(\lambda\) is a weighting coefficient.