Sorting networks and their applications (1968)

#Sorting Algorithm

January 14, 2024

A sorting network is a network of comparison elements with 2 indegree and 2 outdegree that sorts a list in ascending or descending order. A comparison element receives two numbers and outputs the smaller one to one output and the larger one to the other output. Odd-even merging networks and Bitonic sorters are sorting networks proposed in Sorting networks and their applications. They can sort $2^p$ elements with $\ln (\frac{1}{2})p(p+1)$ steps. Their processing is independent of the values and is easy to run on the GPU because it does not change the output location in memory based on input data values.

Odd-even merging networks arrange two ascendingly-ordered numbers into one ascending-ordered list. In the following figure, the odd-even merging network merges $a$ and $b$ into $c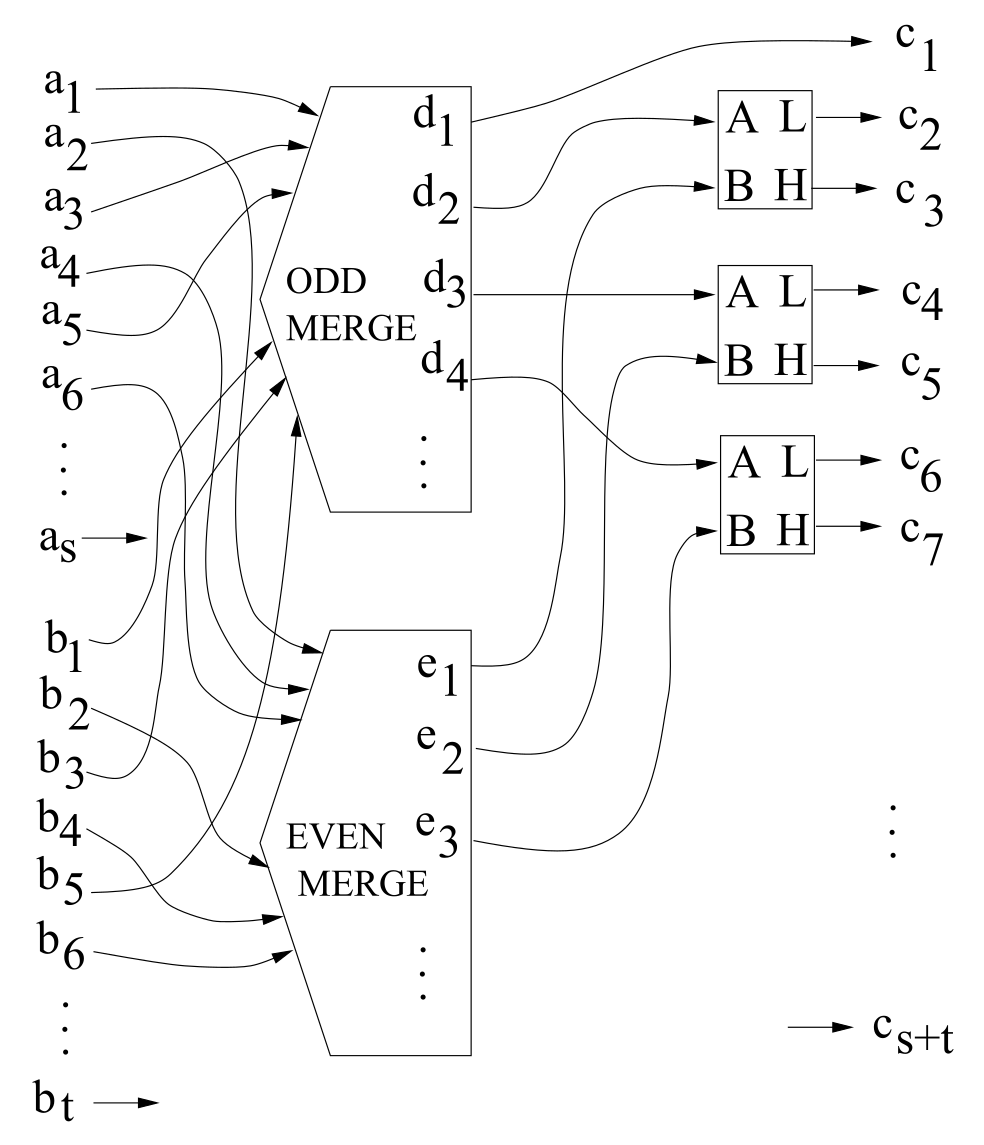$. The rectangle enclosing A, B, L, H is a comparison element. It receives two numbers over A and B and emits their minimum on L and their maximum on H. In the figure, ODD-MERGE (EVEN-MERGE) takes the odd-indexed (even-indexed) numbers of the two input lists and sorts them using a small odd-even merging network. The “s by t” merging network then compares the outputs of these small merges. The lowest output of the odd merge becomes the lowest number of the final list. The $i^{\textit{th}}$ output of the even merge is compared with the $i+1^{\textit{th}}$ output of the odd merge to form the $2i^{\textit{th}}$ and $2i+1^{\textit{th}}$ numberos of the final list. A list is bitonic if the first elements are sorted in ascending order and the remaining elements are sorted in descending order. When the bitonic sort receives a bitonic list of $2n$ elements, $a_1, a_2,\dots ,a_{2n}$, it constructs the following two bitonic lists of $n$ elements by comparing $a_i$ with $a_{n+i}$. $$ \begin{align*} \min(a_1, a_{n+1}), \min (a_2, a_{n+2}), \dots , \min (a_n, a_{2n})\\ \max(a_1, a_{n+1}), \max (a_2, a_{n+2}), \dots , \max (a_n, a_{2n}) \end{align*} $$ Any $\min(a_i, a_{n+i})$ is smaller than any $\max(a_i, a_{n+i})$, and the botonic sorter constructs the final list by concatenating the two smaller lists of $n$ elements. The following figure illustrates a bitonic sorter with $2n$ elements. 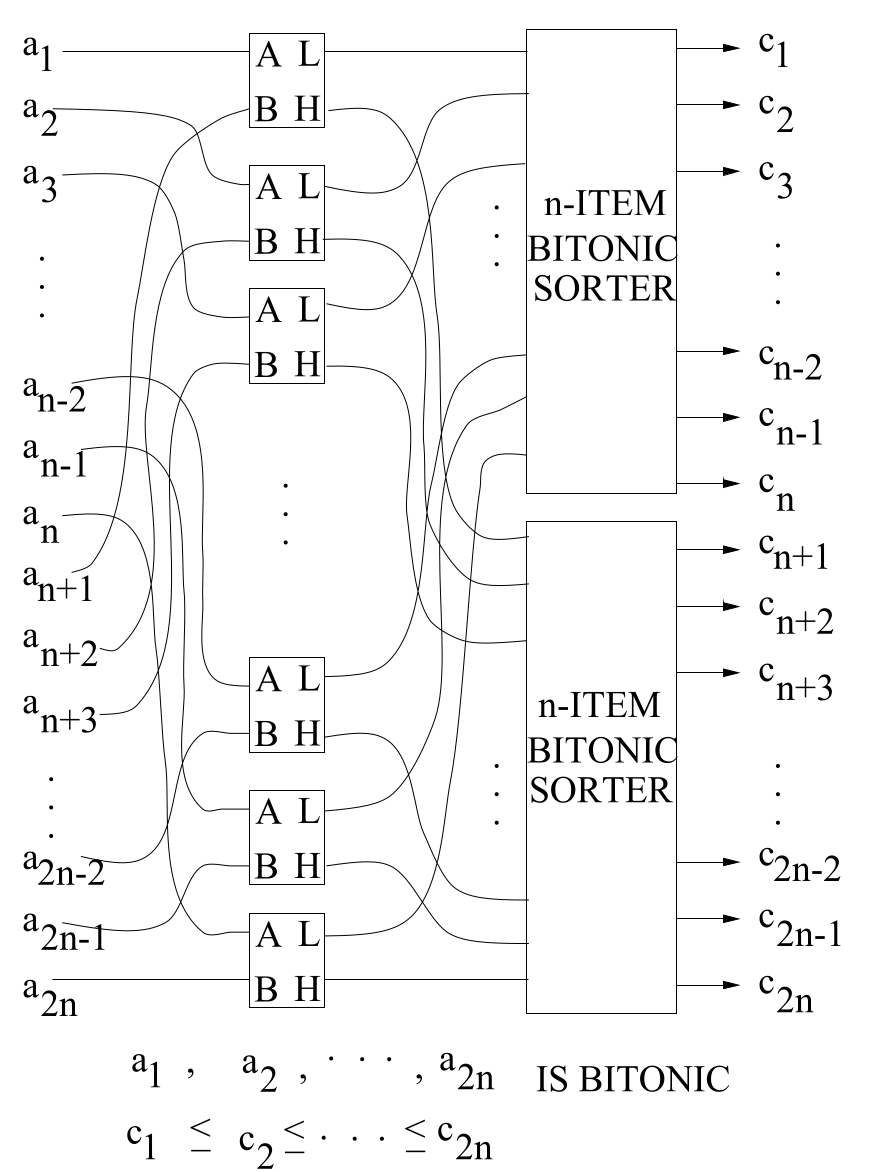bitonic

The figures are cited from Sorting networks and their applications.