論文メモ A STRUCTURED SELF-ATTENTIVE SENTENCE EMBEDDING
May 16, 2020概要
自己注意機構をもちいて、可変長の文を埋め込み行列に変換するアーキテクチャを発表した論文である。 埋め込み行列の各行は、それぞれ文中の異なる箇所の意味を反映する。 アーキテクチャは2つの構成からなり、入力から出力にむかい双方向LSTMを、次に自己注意機構をもつ。 自己注意機構を導入した背景は、回帰結合型のネットワークでは、全ての時刻わたって入力の意味を保持することは難しく、また不要であるという著者らの仮説である。 3つの実験により、文の分散表現を獲得する先行研究と比較し、自己注意機構の効果が確認された。 注意機構は複数のベクトルのどれを重視するかを学習できるため、埋め込まれた文の箇所を可視化できることも示した。
アーキテクチャ
概要
アーキテクチャは、双方向LSTMと自己注意機構の2つのパートからなる。
感情分析の実験のアーキテクチャを以下に図示する。
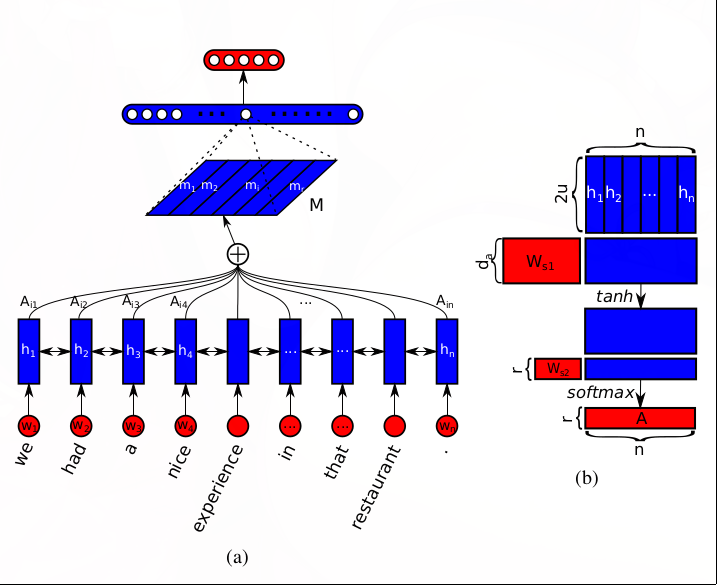 左図は、単語の分散表現の行列となった文を入力し、埋め込み行列に変換し、全結合層を、最後にソフトマックス関数を適用する様子を示す。
行列\(M\)が文の埋め込み行列を表す。
右の図は、自己注意機構であり、双方向LSTMの出力\(H\)からannotation matrixと呼ばれる行列\(A\)を学習する。
埋め込み行列\(M\)は、\(M=AH\)によって求められる。
左図は、単語の分散表現の行列となった文を入力し、埋め込み行列に変換し、全結合層を、最後にソフトマックス関数を適用する様子を示す。
行列\(M\)が文の埋め込み行列を表す。
右の図は、自己注意機構であり、双方向LSTMの出力\(H\)からannotation matrixと呼ばれる行列\(A\)を学習する。
埋め込み行列\(M\)は、\(M=AH\)によって求められる。
双方向LSTM
双方向LSTMは、単語のベクトル列で示された文をうけとり、その出力を自己注意機構に渡す。 以降の説明では、入力される文を、\(n\)個の次元数\(d\)の単語のベクトルからなる\(n\times d\)の行列\(S\)と表記する。
$$ S=(\boldsymbol{\rm w\_1}, \boldsymbol{\rm w\_2}, \cdots \boldsymbol{\rm w\_n}) $$\(\boldsymbol{\rm w_i}\)は文の\(i\)番目の単語の埋め込みベクトルを示す。 双方向LSTMによって、文脈依存の情報をもとめる。 隠れ状態のユニット数を\(u\)とする単方向のLSTMをもちいると、時刻\(t\)の順方向、逆方向のLSTMの隠れ状態、\(\overrightarrow{h_t}, \overleftarrow{h_t}\)を連結させた\(h_t\)を行とする\(n\times 2u\)の行列\(H\)をえる。
$$ H=(\boldsymbol{\rm h\_1}, \boldsymbol{\rm h\_2}, \cdots \boldsymbol{\rm h\_n}) $$自己注意機構
annotation matrixは、バイアス項のない2層の多層パーセプトロンであり、次の式であわらされる。
$$fi A=\text{softmax}(W\_{s2}\tanh(W\_{s1}H^{T})) $$\(d_a\)と\(r\)をハイパーパラメタとして、\(W_{s1}\)は\(d_a\times 2u\)の、\(W_{s2}\)は\(r\times d_a\)の行列のパラメタである。 \(r\)は、注意したい文中の箇所数に対応する。 最終的に、埋め込み行列\(M\)は、\(M=AH\)により、\(r\times 2u\)の行列になる。
埋め込み行列に反映された文の位置の可視化
\(A\)は\(r\times n\)の行列であり、列は各単語がどれだけ埋め込みベクトルに反映されたかを示す。 例えば、行ベクトルを足し合わせ、ノルムを1で正則化したうえで、タスクにおける単語の重要度合いをヒートマップで示すことができる。
正則化
埋め込みベクトルが特定の箇所に注意しすぎないように、正則化を適用することもできる。 その場合、\(P\)をもとのロスに加算して学習する。
$$ P=\mid\mid (AA^T-I)\mid\mid\_{F}^2 $$- 論文をこちらからダウンロードできます。
- 画像は論文から引用されています。