Billion Scale Similarity Search With GPUs (2017)
January 1, 2024Billion-scale-similarity search with GPUsは、IVFADCによる量子化とBatcherのバイトニックソートを利用したGPUで実行するL2ノルムの近似最近傍探索である。 実装は、OSSのfaissとして公開されている。
\(l\)個のデータベースにあるベクトル\([y_i]_{i=0:l}\)の中からクエリ\(x\in\mathbb{R}^d\)の最近傍にある\(k\)個の集合\(L\)に近い要素を、近似的に求める。
$$ L=\text{k-}\argmin\_{i=0:l}||x-y\_i||\_2 $$IVFADCは、\(\mathbb{R}^d\)から\(\mathbb{R}^d\)の真部分集合に写す2つの関数でデータベースベクトルを量子化する。
$$ y\approx q(y) = q\_1(y) + q\_2(y-q\_1(y)) $$関数\(q_1\): \(\mathbb{R}^d\rightarrow \mathcal{C}_1\subset \mathbb{R}^d\)はcoarse quantizer, 関数\(q_2\): \(\mathbb{R}^d\rightarrow \mathcal{C}_2\subset \mathbb{R}^d\)はfine quantizerとよばれる。 \(q_2\)は\(q_1\)を適用した結果と\(y\)の残差をエンコードする。 IVFADCは、\(q_1\)で\(y\)の近傍にある\(\mathcal{C}_1\)で写されるデータベースベクトルのみを検索対象に限定する。 まず、\(y\)の最近傍にある\(\tau\)個の\(\mathcal{C}_1\)の部分集合\(L_{\text{IVF}}\)を求める。
$$ L\_{\text{IVF}}=\tau-\argmin\_{c\in\mathcal{C}\_1}||x-c||\_2 $$次に、\(L_\text{IVF}\)にあるデータベースベクトルの量子化された値とクエリ\(x\)を比較し、\(k\)個の最近傍の集合\(L_{\text{IVFADC}}\)を求める。
$$ L\_{\text{IVFADC}}=k-\argmin\_{i=0:l\ \text{s.t.}\ q\_1(y\_i)\in L\_{\text{IVF}}}||x-q(y\_i)||\_2 $$\(q_1\)は\(|\mathcal{C}_1|\approx \sqrt{l}\)に設定したk-meansで決められ、\(q_2\)にはproduct quantizerが使われる。 Product quantizerは、\(y\)を\(d\)の偶数の約数\(b\)単位に分割\((y=[y^0\dots y^{b-1}])\)し、分割したサブベクトルごとに量子化する。 サブベクトルは1バイトに収まる\([0,255]\)の値に変換され、量子化された値をビットシフトすることで、\(q_2(y)\)の値\(q_2(y)=q^0(y^0)+256\times q^1(y^1)+\dots + 256^{b-1}\times q^{b-1}(y^{b-1})\)が求まる。
量子化されたデータベースベクトルとクエリ間の距離を求めたら、Batcherのバイトニックソートでクエリの最近傍にある\(k\)個のベクトルを見つける。
以下の論文から引用した図はソートの様子を示す。
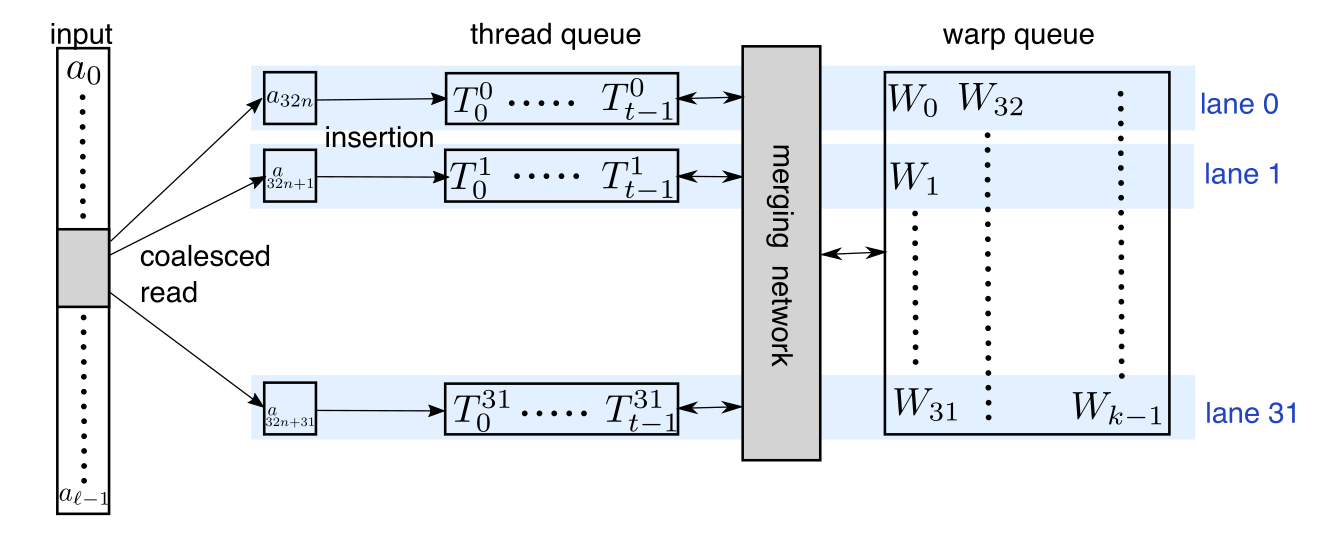 \([a_i]_{i=0:l}\)はソート対象であり、\([T^j_i]_{i=0:t}\)は降順の優先度付きキュー(\(T^j_{i}\ge T^j_{i+1}\))を示す。
\([W_i]_{i=0:k}\)は調べた中で最も距離の小さい\(k\)個の要素を表す。
\(a\)が\(T^j_0\)より大きければ\(a\)が\(k\)個の最近傍ではないように、\(T^j_0\)は任意の\(W_i\)よりも大きくなるように管理される。
\([a_i]_{i=0:l}\)はソート対象であり、\([T^j_i]_{i=0:t}\)は降順の優先度付きキュー(\(T^j_{i}\ge T^j_{i+1}\))を示す。
\([W_i]_{i=0:k}\)は調べた中で最も距離の小さい\(k\)個の要素を表す。
\(a\)が\(T^j_0\)より大きければ\(a\)が\(k\)個の最近傍ではないように、\(T^j_0\)は任意の\(W_i\)よりも大きくなるように管理される。