Catalan Numbers(2016)
July 29, 2023カタラン数は、いくつかの組合せの問題の解で知られる自然数の系列である。 \(n\)個の対応する括弧"(, )“からなる文字列の組合せの数や、一辺の長さが\(n\)の格子の左上から右下への対角線より上を通る最短経路の数は、\(n\)番目のカタラン数である。 このページでは、この2つの問題の解がカタラン数であるとして、漸化式と二項係数の2つの形式によるカタラン数の一般項を求める。
対応する括弧の意味を明確にする。 文字列を左から順に読んでいき、0で初期化された変数に対して、(があれば1を加算、)があれば1を減算する。 文字列を読み終えたときの変数の値が0かつ、変数が一度も負にならないとき、文字列のすべての括弧は対応関係にあるとみなす。
対応する括弧の数\(n\)が0であれば組合せの数は0, 1であれば1, 2であれば2, 3であれば5とつづく。 つまり、括弧の数が\(n\)であるときの組合せの数は、\(n\)番目のカタラン数\(C_n\)である。
この括弧の問題から、カタラン数\(n\)の漸化式による一般項を求める。 \(n\)より小さいカタラン数を\(C_i (i < n)\)とおく。 n個の対応する括弧からなる空でない文字列を”(A)B"とする。 A, Bは\(n\)個よりも小さい文字列である。 Aにある括弧の数が\(k\)であるとき、Bの括弧の数は\(n-1-k\)である。 \(k\)がとりあえる値の範囲は\(0\)以上\(n-1\)以下であるからカタラン数\(C_n\)は $$ C_n = C_{n-1}C_0 + C_{n-2}C_1 + \cdots + C_1C_{n-2} + C_0C_{n-1} $$ となる。
今度は、格子を例題に、二項係数によるカタラン数の表現を求める。 縦の長さが\(n\), 横の長さが\(m\)の格子の左上から右下への最短経路は、\(n+m\)回の距離1の移動からなり、そのうち\(n\)個が下への移動である。 そのため、最短経路の数は\(\binom{n+m}{n}\)になる。
左上から右下への対角線を一回でも横切る経路の数が分かれば、すべての最短経路の数との差からカタラン数を求められる。
すべての対角線を横切る経路は、以下の図にあるPのような、最初に対角線を横切った直後の点を通る。
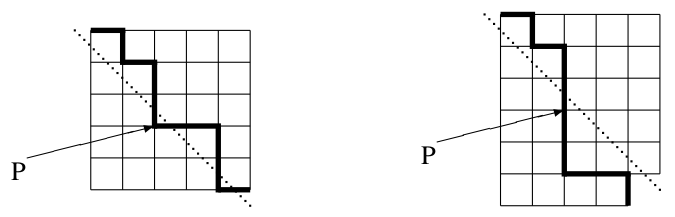 右図のように、この点より右下にある格子を対角線を軸に反転すると、横切る経路は\(n+1\)回の下への移動と\(n-1\)回の右への移動からなる。
以上からカタラン数は、二項係数で
$$
C_n = \binom{2n}{n} - \binom{2n}{n+1}
$$
とも表せる。
右図のように、この点より右下にある格子を対角線を軸に反転すると、横切る経路は\(n+1\)回の下への移動と\(n-1\)回の右への移動からなる。
以上からカタラン数は、二項係数で
$$
C_n = \binom{2n}{n} - \binom{2n}{n+1}
$$
とも表せる。
図を参考文献の論文から引用しました。