Coverage Is Not Strongly Correlated With Test Suite Effectiveness (2014)
March 3, 2025コードカバレッジに対する批判を散見する。 たとえば、Googleのソフトウェアエンジニアリングの11.2.4節「コードカバレッジについてもメモ」には、コードカバレッジに対する2つの批判がある。 まず、最低限満たすべきコードカバレッジを設定すると、すぐに水準を下回るコードがすぐにリポジトリに取り込まれはじめる。 次に、テストカバレッジが保証するのはテストがコードが実行することだけであり、実行したコードにあるバグを見つけるとは限らない。
このような経験則や論理による批判にくらべると、実験にもとづく批判を見聞することは少ないだろう。 Coverage Is Not Strongly Correlated with Test Suite Effectivenessは、ICSE 2024でMost influential paper ICSE N-10に選ばれた文献で、OSSのテストカバレッジとテストの有効性の相関を調べた。 Apache POI, Closure, HSQLDB, JFreeChart, Joda Timeのコードベースをミューテーション解析し、テストケースの有効性を、テストケースを失敗させた変異体の数で定量化した。 テストケースの数とテストスイートのカバレッジは、有効性との間に中から高の相関があった。 一方、テストケースの数を固定すると、カバレッジと有効性の相関は低から中に減少した。
調査結果の新規性と一般性のために、5つのプロジェクトはコードベースの大きさと開発の活発状況から選ばれた。 大きさの目安は、100,000行以上のソースコード、1,000以上のテストケースだった。 また、データ収集の自動化のために、ビルドツールにAnt, テストフレームワークにJUnitが使わていることも条件にあった。 Apache POIは、MicrosoftのドキュメントのためのAPI, ClosureはJavascriptを最適化するコンパイラ、HSQLDBはRDBMS, JFreeChartはチャート描画のライブラリ、Joda-TimeはJava8以前に日付と時刻のクラスの代用として使われていたライブラリである。
テスト数を固定したときのカバレッジと有効性の相関を測るために、JUnitの@Testがついたメソッドを非復元抽出した。
抽出したテストケースの集合をテストスイートとみなし、3, 10, 30, 100, 300, 1000, 3000個のテストケースからなるテストスイートを組成した。
有効性と比較するカバレッジは、C0, C1, MCCの3種類で、後者ほど充足条件が厳しい。 C0は、命令網羅率ともいい、テストスイートが実行した文の割合でカバレッジとする。 C1は、分岐網羅率であり、実行した分岐の割合でカバレッジを測定する。 MCCは、\(n\)個の真偽値型の変数からなる条件式に対して\(2^n\)個のテストケースを充足に求める測定方法で、航空機搭載システムの品質保証規格DO-178Bで使われる。
テストケースの有効性を評価するために、ミューテーション解析のツールPITで人工的な欠陥をコードベースに注入した。 ミューテーション解析は、定数や不等式の変更などの小さな欠陥をコードに加える。 欠陥を注入されたコードベースは変異体 (mutator) とよばれる。 テストケースを変異体に対して実行し、テストケースが失敗できるかでテストスイートを評価する。
実験における有効性の測り方は2つある。 ひとつは、組成したすべての変異体の数に対してテストスイートが検知できた変異体の数の割合であり、これを非正規化された有効性とよんだ。 もうひとつは、正規化された測定方法であり、テストスイートが実行した行に欠陥が注入された変異体の数に対して検知できた変異体の数の割合を測る。
テストケースの数と正規化された有効性の相関を単回帰分析で求めた。
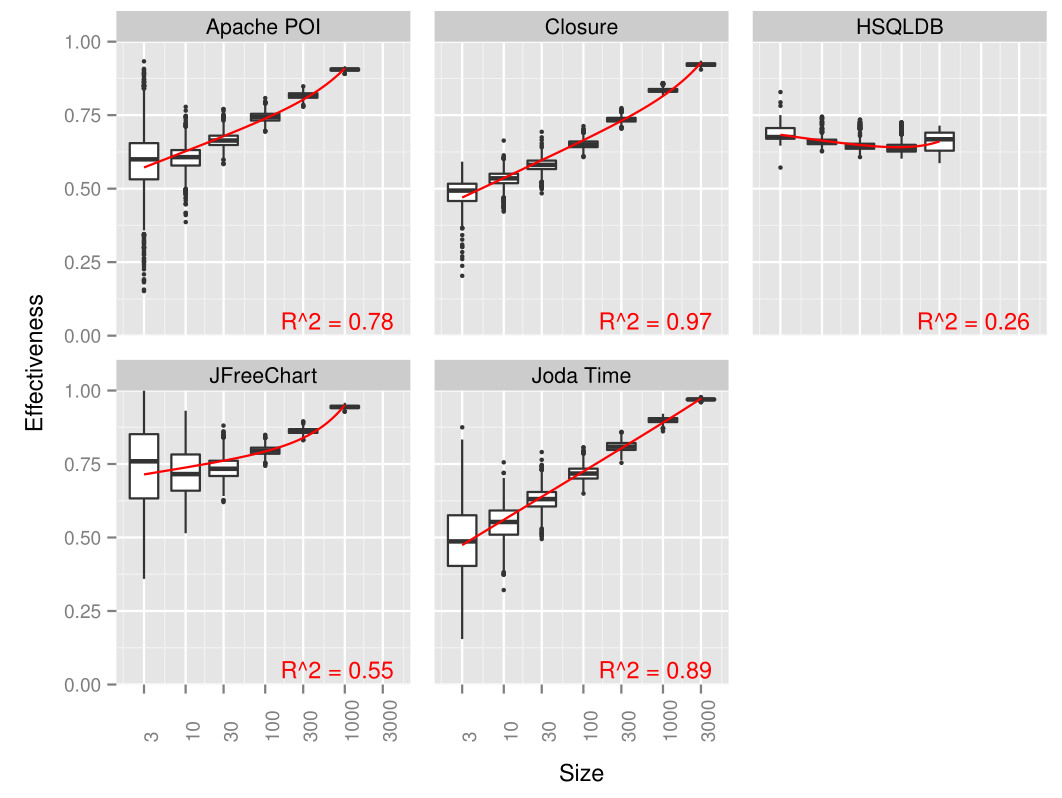
以下に、Rのlm関数の計算結果をプロットした図を示す。
\(R^2\)は自由度調整済み決定係数を表す。
文献には、自由度調整済み決定係数とあるが、同時に、\(R\)を相関係数とも書いている。
また、単回帰分析であるため、\(R^2\)は決定係数ととらえてよいだろう。
HSQLDBを除けば、テストケースの数と正規化された有効性には中から高い相関がみられた。
カバレッジと有効性の相関には、ケンドールの順位相関係数\(\tau\)を使う。 \(i\)番目のテストスイートのカバレッジを\(x_i\), 有効性を\(y_i\)とする\(n\)個のサンプルがあるとき、\(\textit{sgn}\)を符号関数とすると、\(\tau\)は
$$ \tau = \frac{n\sum\_{iいずれのカバレッジを採用しても、カバレッジと有効性の間に相関に顕著な違いはなかった。
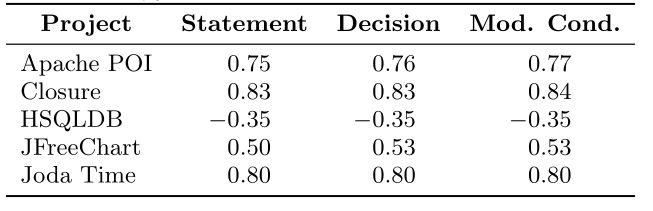
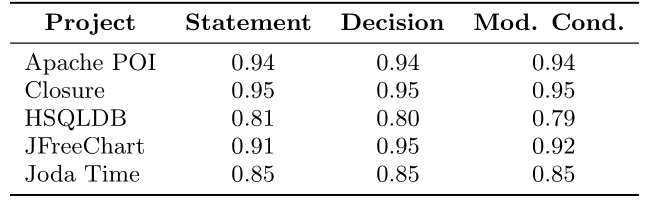
以下の表は、文献からにあるカバレッジと有効性の相関係数を示す。
上が正規化された有効性であり、下が正規化されていない有効性との相関に対応する。
Joda Timeの相関係数は正規、非正規どちらにおいても、すべてのカバレッジで等しい。
カバレッジを厳密にしても、テストの有効性の測定精度の改善にはならない結果になった。
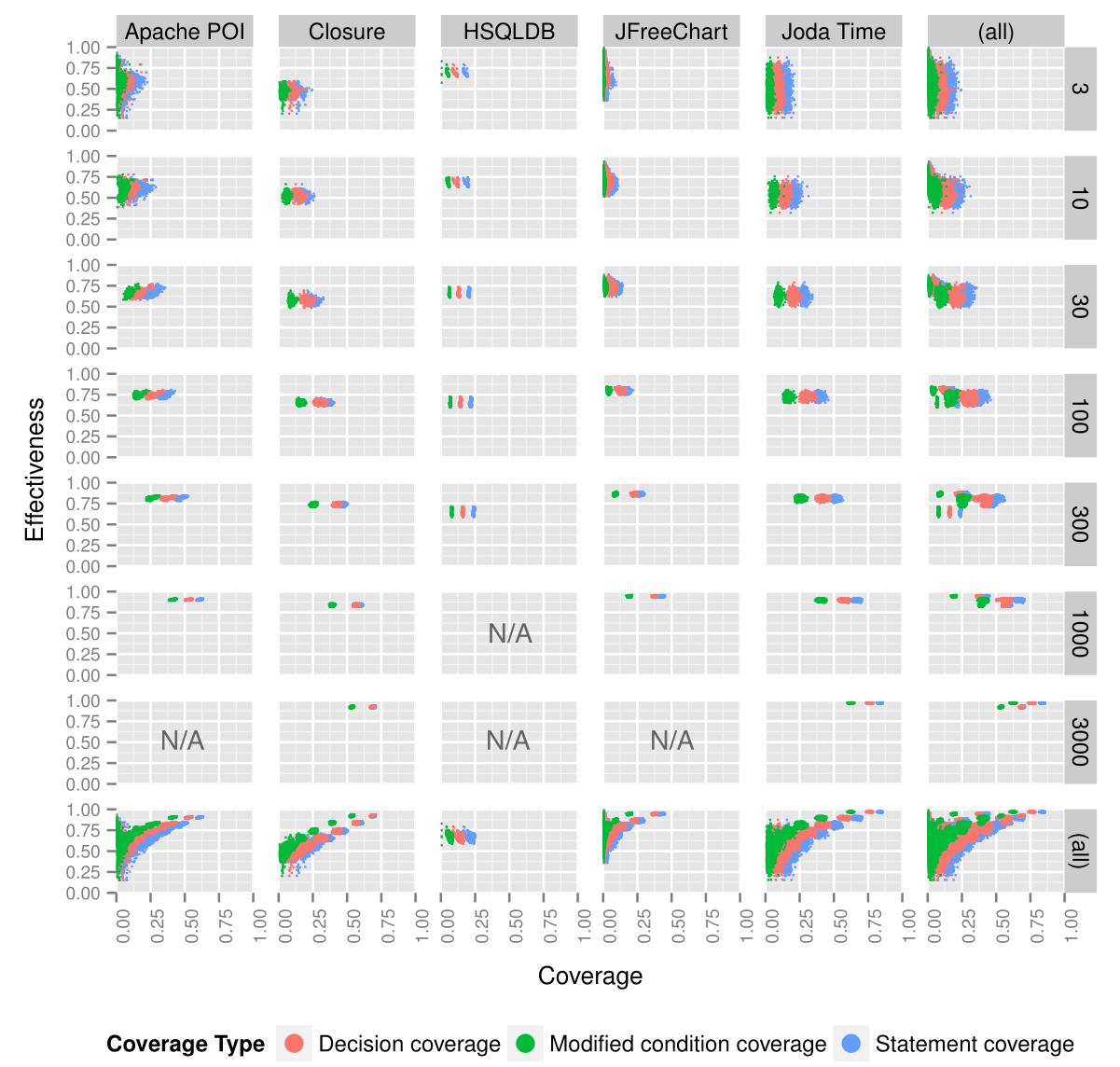
テストケースの数を揃えたテストスイート間では、カバレッジと正規化した有効性の間の正の相関が減少した。
文献から引用した下の図は、テストケースの数ごとに、カバレッジと正規化した有効性の相関を示す。
テストケースを固定した1から7行目の図には、正の相関を示す右方上がりのプロットはみられない。
冒頭で紹介したGoogleのソフトウェアエンジニアリングの節は、カバレッジの高さがテストスイートの有効性の高さを含意しないことで、カバレッジに対して論理的に批判的な態度であった。 同じ論理で、テストケースの数の多さからもテストスイートの有効性を主張することはできない。 しかし、単回帰分析の結果では、テストケースの数と有効性の間に中から高い相関がみられた。 論理よりもデータの傾向を尊重するとしたら、テストスイートの効率性を定量的に測りたければ、カバレッジよりもテストケースの数で測るべきなのだろう。