論文メモ End-to-end Neural Coreference Resolution
October 10, 2020ニューラルネットワークによる共参照解析の手法で、End-to-Endとあるように、構文解析やルールベースの参照表現に頼らず、先行研究を上回る性能を発揮した。 文書中の全ての単語系列を参照表現の候補とみなし、ある単語系列の組が照応関係にある確率の分布を学習する。
タスクは、\(T\)個の単語からなる文書\(D\)を入力として、各単語系列\(i\)の先行詞\(y_i\)を推定するものになる。 実験のデータセットはCoNLL-2012 shared taskであり、単語のほか、データセットにある注釈のgenreとspeakerも特徴につかわれる。 とりえる単語系列の数を\(N=\frac{T(T+1)}{2}\)とおく。 \(\mathcal{Y}(i)=\{\epsilon,1,\dots i-1\}\)は単語系列\(i\)の先行詞の候補\(y_i\)の集合を示す。 \(\epsilon\)は、\(i\)が参照表現でないか、参照表現であっても既出のどの単語系列とも照応関係にないことを意味する。 このとき、モデルは、次の確率分布\(P(y_1,\dots ,y_N\mid D)\)を学習する。 これは、各単語系列の先行詞についての確率分布の積になっている。
$$ \begin{align} P(y\_1, \dots y\_N\mid D)&=\prod\_{i=1}^{N}P(y\_i\mid D)\\\\\ &=\prod\_{i}^{N}\frac{\exp (s(i, y\_i))}{\sum\_{y'\in \mathcal{Y}(i)}\exp(s(i, y'))} \end{align} $$\(s(i,j)\)は、単語系列\(i, j\)の照応関係のスコアを示す。 \(s_m(x)\)は\(x\)が参照表現かを示し、\(s_a(i,j)\)は\(j\)が\(i\)の先行詞かを示すスコアである。 計算量を削減する場合、\(s_m(x)\)に閾値をもうけて、候補とする単語系列の数を減らす。
$$ s(i,j)= \begin{cases} 0&j=\epsilon\\\\\ s\_m(i)+s\_m(j)+s\_a(i,j)&j\neq \epsilon \end{cases} $$次の2つの図は、ネットワークアーキテクチャ全体を示す。 \(s_m(i)\)は、順伝播ネットワーク\(\text{FFNN}_m\)に単語系列の分散表現\(\boldsymbol{g}_i\)をあたえた出力とパラメタ重み\(\boldsymbol{w}_m\)の積である。
$$ s\_m(i)=\boldsymbol{w}\_m\cdot \text{FFNN}\_m(\boldsymbol{g}\_i) $$\(s_a(i,j)\)は、順伝播ネットワーク\(\text{FFNN}_a\)に2つの単語系列の分散表現とgenre, speakerの特徴ベクトル\(\phi (i, j)\)をあたえた出力とパラメタ\(\boldsymbol{w}_a\)からなる。 \(\circ\)は要素同士の乗積をさす。
$$ s\_a(i,j)=\boldsymbol{w}\_a\cdot\text{FFNN}\_a([\boldsymbol{g}\_i,\boldsymbol{g}\_j,\boldsymbol{g}\_i\circ\boldsymbol{g}\_j,\phi(i,j)]) $$単語系列の分散表現\(\boldsymbol{g}_i\)は、双方向LSTMに単語の分散表現\(\{\boldsymbol{x}_1,\dots , \boldsymbol{x}_T\}\)からつくられる。 \(\{\boldsymbol{x}_1,\dots , \boldsymbol{x}_T\}\)は、学習済みの単語の分散表現と文字単位の1次元CNNの出力からなる。 このとき単語\(\boldsymbol{x}_t\)に対応する双方向LSTMによる分散表現を\(\boldsymbol{x}^{*}_t\)とおく。 単語系列の始点をSTART(\(i\)), 終点をEND(\(i\))とすると、\(\boldsymbol{g}_i\)は、次の式で計算される。
$$ \begin{align} \alpha\_t&=\boldsymbol{w}\_{\alpha}\cdot\text{FFNN}\_{\alpha}(\boldsymbol{x}^{*}\_{t})\\\\\ \alpha\_{i,t}&=\frac{\exp(\alpha\_t)}{\sum^{\text{END}(i)}\_{k=\text{START}(i)}\exp(\alpha\_k)}\\\\\ \boldsymbol{\hat{x}}\_i&=\sum^{\text{END}(i)}\_{t=\text{START}(i)}\alpha\_{i,t}\cdot\boldsymbol{x}\_t\\\\\ \boldsymbol{g}\_i&=[\boldsymbol{x}\_{\text{START}(i)}^{\star},\boldsymbol{x}\_{\text{END}(i)}^{\star},\boldsymbol{\hat{x}}\_{i},\phi (i)] \end{align} $$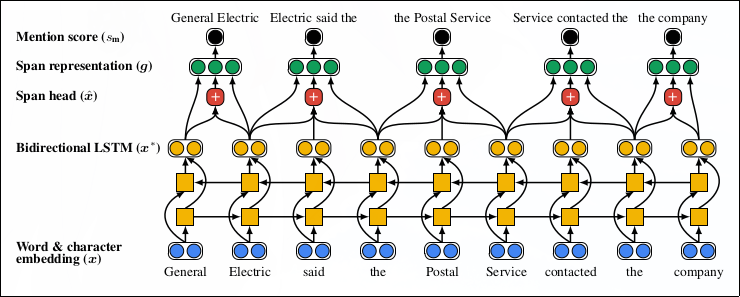
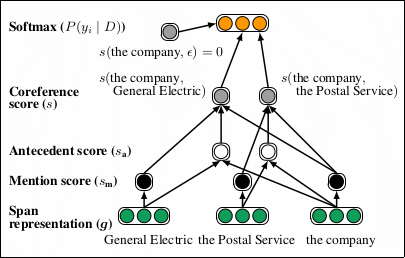
教師データGOLDにある単語系列\(i\)を先行詞とする集合をGOLD(\(i\))とする。 ただし、\(i\)が集合に所属していないか計算量の都合でGOLDにある先行詞が枝刈りされいれば、GOLD\((i)=\{\epsilon\}\)とする。 このとき、目的関数は次の式になる。
$$ \log\prod^N\_{i=1}\sum\_{\hat{y}\in\mathcal{Y}(i)\cap\text{GOLD}(i)}P(\hat{y}) $$- 論文をこちらからダウンロードできます。