論文メモ Organization and Maintenance of Large Ordered indexes

February 27, 2021

1972年に発表されたB木のオリジナルの論文。 $I$をインデックスの大きさ、$k$をハードウェア依存の値とすると、検索、挿入、削除の時間計算量は$\log_kI$になる。ここでのインデックスは、固定長の$(x, \alpha)$を要素とする連想配列で、最大$2k$個のキーを格納できる連続したページ上にある。 $\alpha$には、データを保存した1つ以上のレコードへのポインタが格納される。

$h$を非負の整数、$k$を自然数とすると、空の木や次の3つの条件をみたす木をB木という。

ルートから任意の葉までの長さが$h$であり、ルートから葉までの経路のノード数が$h$になる。
ルートと葉以外は少なくとも$k+1$個の子をもつ。ルートは葉であるか、少なくとも2つの子をもつ。
各ノードがもつ子の数は高々$2k+1$個。

冒頭の時間計算量で検索、挿入、削除を実現するために、以下の3条件が成り立つようにインデックスを構成する。

ルートページは1以上$2k$以下のキーを、それ以外のページは$k$以上$2k$以下のキーをもつ。
葉以外のページにあるキーの数が$l$であれば、そのページは$l+1$個の子ページをもつ。
各ページの$l$個のキーは昇順に並び、ページは子ページへのポインタ$p_0, p_1, \dots p_l$をもつ。葉ページでは子ページのポインタは未定義になる。

以下に性質をみたすページを図示する。 page

$P(p_i)$をポインタ$p_i$がさすページとし、$K(p_i)$を、$P(p_i)$をルートとする最大の部分木に含まれるキーの集合とする。このとき、B木は次の3つの性質をみたす。

$$ \begin{align} (\forall y\in K(p\_0))(y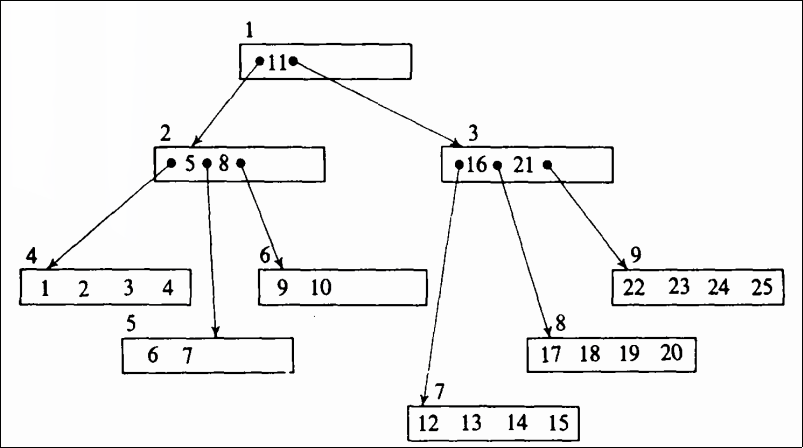 以下に、これらの性質をみたすB木を例示する。 tree

キーを挿入するとき、挿入先のページ$P$が満杯であればページを分割する。はじめに、キーとポインタからなる次の配列をつくる。

$$ p\_0, (x\_1, p\_1), (x\_2, p\_2),\dots ,(x\_{2k+1}, p\_{2k+1}) $$

次に、この配列の一部

$$ p\_0, (x\_1, p\_1),\dots ,(x\_{k}, p\_{k}) $$

で$P$をおきかえ、新しいページ$P’$に

$$ p\_{k+1}, (x\_{k+2}, p\_{k+2}), (x\_{k+3}, p\_{k+3}),\dots ,(x\_{2k+1}, p\_{2k+1}) $$

を代入する。その後、$Q$を$P$の親ページとして$Q$に$(x_{k+1}, p’)$を挿入し、$P’$を$P$の兄弟にする。なお、ポインタ$p’$は$P’$をさす。

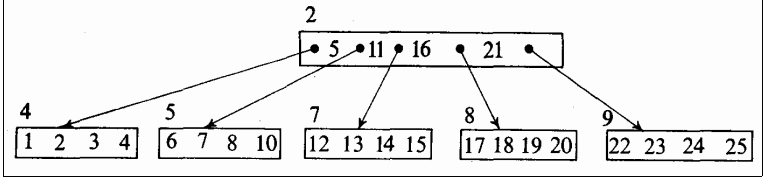
$Q$が満杯であれば、$Q$も分割する。これをくりかえし、分割がルートまで及ぶ場合、$p$と$(x_{k+1}, p’)$をふくむルートページ$Q$をつくる。 $p$と$p’$は、ページ$P, P’$をさす。例えば、$k=2$とすると、以下のB木にキー9を挿入すると、上のB木になる。 tree2

キーを削除するとき、そのキーが葉になければ、単に削除するだけでなく、$P(p_i)$をルートページとする木の中の最小のキーと置きかえなければならない。この最小のキー$x_1$が存在するページを$L$とすると、$x_1$を消すことで$L$にあるキーの数が$k$より少くなりうる。その場合、ページ$L$をさすポインタと隣接するポインタによって参照される兄弟ページと$L$の間でcatenationまたはunderflowという操作をおこなう。

catenationは、隣接するポインタで参照された兄弟ページの合計キー数が$2k$以下のときに兄弟ページを結合する操作をいう。このとき、親ページのエントリが削除されるので、挿入時と同様、catenationはルートページまで伝搬することがある。

合計キー数が$2k$より大きいときは、catenationを実施し、結合されたページを真ん中で分割する。この操作をunderflowという。上にある2つ目のB木からキー9を削除すると、1つめのB木にもどる。

論文をこちらからダウンロードできます。図は、論文から引用しました。