Poly-Encoders: Architectures and Pre-Training Strategies for Fast and Accurate Multi-Sentence Scoring (2019)
February 24, 2024入力系列のラベルを推定できるようにTransformerのエンコーダーをファインチューニングするとき、エンコーディングの仕方に、Cross encoder (Wolf et al.) とBi-encoder (Mazaré et al.) がある。 Cross-encoderは、入力系列とラベルを連結した系列をエンコーダーに入力し、入力系列とラベルのペアのエンベディングからスコアを求める。 Bi-encoderは、入力系列とラベルを別のエンコーダーに入力し、それぞれのエンベディングの内積をスコアとする。
Cross-encoderは予測性能に長け、Bi-encoderは処理速度に優れる。 Cross-encoderは、入力とラベルを連結した系列をエンコーダーに入力するので、Bi-encodersよりも両者の関係をとらえたスコアを出力できる。 Bi-encoderは、ラベルのエンベディングを入力系列ごとに計算しなくてよい。
Poly-encoderは、Cross-encoderの予測性能とBi-encoderの速度の両立するためのエンコーディング法である。 Bi-encoderとおなじように、ラベルを入力系列とは別のエンコーダーでエンコードする。 一方、長さ\(N\)の入力系列をエンコードするときは、まず、エンコーダーの出力した\(N\)個のベクトルをキーとして\(m\ (<N)\) 個の注意機構に入力する。 同時に、ランダムな値で初期化したクエリ\(c_i\)を各注意機構に入力する。 その結果、えられた\(m\)個のエンベディングをキー、ラベルのエンベディングをクエリとして後続の注意機構に入力し、その出力をラベルの候補に対する入力系列のエンベディングとしてあつかう。 そして、ラベルのエンベディングと入力系列のエンベディングの内積をスコアとみなす。 以上のように、入力系列とラベルの候補の両方を入力する注意機構を減らすことで、計算量が削減されている。
Cross-encoderは、事前学習とおなじく、BERTの[SEP]に相当する区切りのトークンを入力系列 \(\textit{ctxt}\) とラベルの候補\(\textit{cand}\)の間に挿入し、エンコーダに入力する。
以下の図は、論文にあるCross-encoder, Bi-encoder, Poly-encoderのアーキテクチャを表す。
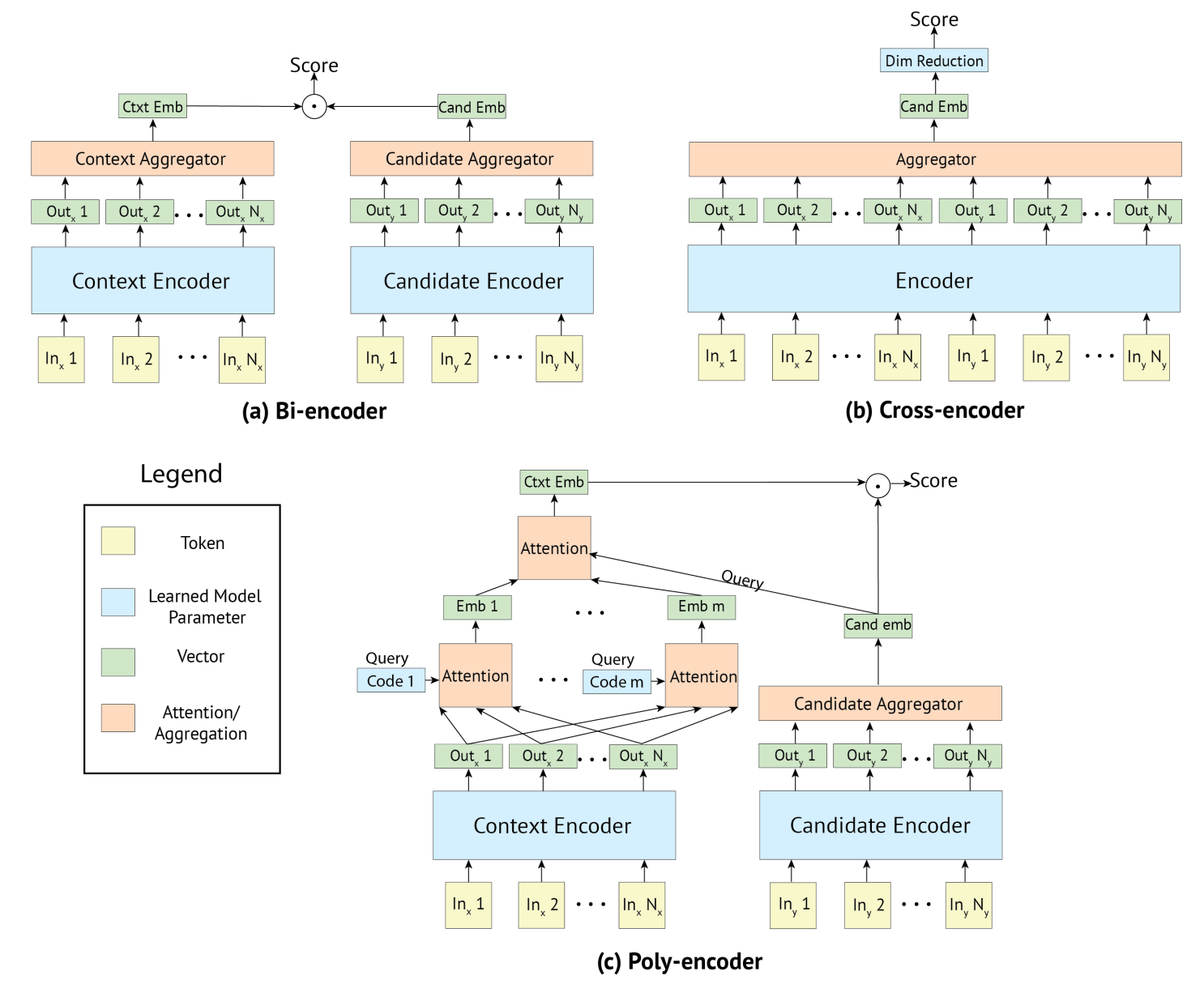 長さ\(N\)の入力系列をエンコーダー\(T\)に入力したときの出力を\(h_1,\dots h_N\)とすると、BERTの
長さ\(N\)の入力系列をエンコーダー\(T\)に入力したときの出力を\(h_1,\dots h_N\)とすると、BERTのCLSとおなじように、先頭のトークンのベクトル\(h_1\)を入力系列とラベルのペアのエンベディングとしてあつかう。
\(\textit{first}\)をベクトルの系列から最初のベクトルを取り出す関数とすると、以上の手順を以下の式で表せる。
そして、入力系列とラベル候補のエンベディング \(y_{\textit{ctxt,cand}}\)に全結合層\(W\)を適用した結果をスコアとみなす。
$$ s(\textit{ctxt}, \textit{cand}\_i) = y\_{\textit{ctxt}, \textit{cand}\_i}W $$損失関数には交差エントロピーをつかい、\(\textit{cand}_1\)を\(\textit{ctxt}\)の正解ラベル、それ以外の\(\textit{cand}_i\)を負例のラベルとして、\(s(\textit{ctxt}, \textit{cand}_1), \dots , s(\textit{ctxt}, \textit{cand}_n)\)を入力する。
Bi-encoderは入力系列とラベルの候補を別のエンコーダーに入力するので、事前学習時とファインチューニングでエンコーダーへの入力の仕方がことなる。
その上で事前学習と入力を似せるように、入力系列とラベルの候補をどちらも区切のトークンSEPで囲む。
また、トークンが系列とラベルのどちらかを示すBERTのセグメントには、事前学習時の系列に利用した値を指定する。
Cross-encoderとおなじく、Bi-encoderも、エンコーダーの出力するベクトルの系列の先頭ベクトルを、入力系列やラベルのエンベディングとみなす。 そして、両者のエンベディングの内積をスコアとみなす。
Poly-encoderは、エンコーダーが出力する長さ\(N\)のベクトルの系列\(h_1,\dots h_N\)をキーとして、\(m\)個の注意機構に入力する。また、注意機構\(i\)には、ランダムな値で初期化された\((c_1,\dots,c_m)\)のうち\(c_i\)もクエリとして入力される。 クエリは図のCode \(i\)に該当する。
$$ y^i\_{\textit{ctxt}}=\sum\_jw^{c\_i}\_jh\_j\ \ \ \ \text{where}\ \ \ \ (w\_1^{c\_i},\dots , w\_N^{c\_i}) = \text{softmax}(c\_i\cdot h\_1,\dots , c\_i\cdot h\_N) $$次に、\(m\)個の注意機構の出力\(y^i_{\textit{ctxt}}\)をキー、ラベルのベクトルをクエリとして後続の注意機構に入力する。
$$ y\_{\textit{ctxt}}=\sum\_iw\_iy^i\_{\textit{ctxt}}\ \ \ \ \text{where}\ \ \ \ (w\_1,\dots ,w\_m) = \text{softmax}(y\_{\textit{cand}\_i}\cdot y^1\_{\textit{ctxt}}, \dots , y\_{\textit{cand}\_i}\cdot y^m\_{\textit{ctxt}}) $$そして、注意機構の出力\(y_{\textit{ctxt}}\)とラベルの候補\(y_{\textit{cand}_i}\)の内積\(y_{\textit{ctxt}}\cdot y_{\textit{cand}_i}\)をスコアとする。