論文メモ Robust Random Cut Forest Based Anomaly Detection On Streams
March 12, 2021Robust Random Cut Forest(RRCT)はストリームデータ向きの異常検知の手法で、Amazon SageMakerから提供されている。 バッチデータと違い、ストリームデータは新たなデータが随時追加、修正される。 RRCTは、特徴の値でデータを2分するノードからなる木の集合であり、データを追加したときに木の集合であるモデルを大きく複雑するものを異常と判定する。
RRCTは、ランダムに選ばれた特徴がとりえる値をランダムに選び、その大小でデータを二分する木の集合からなる。 データセット\(S\)から次の手順でRRCTを構築できる。
- \(l_i=\max_{x\in S}x_i-\min_{x\in S}x_i\)として\(\frac{l_i}{\sum_jl_j}\)にしたがう確率でランダムに特徴を選ぶ。
- 一様分布\([\min_{x\in S}x_i,\max_{x\in S}x_i]\)にしたがうものとして、二分する境界値\(X_i\)をランダムに選ぶ。
- \(S_1=\{x\mid x\in S,x_i\le X_i\}\)と\(S_2=S\backslash S_1\)で分割し、再帰的に\(S_1\), \(S_2\)に本手順を適用する。
RRCTは、データの追加前後におけるモデルの複雑さの変化で、データの異常、正常を推定する。
複雑さの指標には、以下の図のように、根から各葉に到達するための分岐方向をビット列で表したときのビット数の総和をつかう。
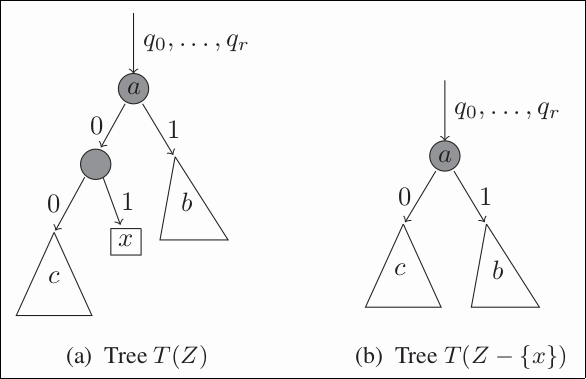 \(T\)を木、\(Z\)をデータ集合、\(y\)を\(Z\)の要素、\(f(y, Z, T)\)を根から\(y\)に到達するまでの経路を表すために必要なビット数とする。
このとき、\(x\)を\(Z\)から除いたときのモデルの複雑さ\(\mid M(T’) \mid\)を次の式で評価する。
\(T\)を木、\(Z\)をデータ集合、\(y\)を\(Z\)の要素、\(f(y, Z, T)\)を根から\(y\)に到達するまでの経路を表すために必要なビット数とする。
このとき、\(x\)を\(Z\)から除いたときのモデルの複雑さ\(\mid M(T’) \mid\)を次の式で評価する。
\(x\)の有無によるモデルの複雑さの変化の期待値を以下の式で算出する。
$$ \begin{align} &\mathbb{E}\_{T(Z)}[\mid M(T)\mid ]-\mathbb{E}\_{T(Z-\\{x\\})}[\mid M(T(Z-\\{x\\})\mid]\\\\ &=\sum\_T\sum\_{y\in Z-\\{x\\}}\mathbb{P}\_r[T]\left(f(y,Z,T)-f(y,Z-\\{x\\},T')\right)\\\\ &+\sum\_T\mathbb{P}\_r[T]f(x,Z,T) \end{align} $$ところが、上の式で外れ値を算出してもロバストにはならない。 外れ値\(p\)の近くに正常なデータがあれば、差異が小さくなり、\(p\)を異常値として判定されない。 そのため、以下の式で、推定対象の\(x\)を含めた\(x\)近辺の部分集合の有無によるモデルの複雑さの変化で、異常値かどうかを推定する。
$$ \mathbb{E}\_{T(Z)}[\mid M(T)\mid ]-\mathbb{E}\_{T(Z-C)}[\mid M(T(Z-C))\mid ] $$最終的には、次の値が高いほど\(x\)が異常であると推定する。
$$ \mathbb{E}\_{S\subseteq Z, T}\left[\max\_{x\in C\subseteq S}\frac{1}{\mid C\mid}\sum\_{y\in S-C}\left(f(y, S, T)-f(y,S-C,T'')\right)\right] $$論文をこちらからダウンロードできます。