Sorting networks and their applications (1968)

#Sorting Algorithm

January 14, 2024

ソーティングネットワークは、入次数と出次数が2のノードからなるグラフを理論にしたソートのアルゴリズムである。ノードは、別々の辺から入力された値の大小関係を比較し、大きい方を一方、小さい方を他方の辺に出力する。 Sorting networks and their applicationsで提案された奇偶マージソートとバイトニックソートは、値によらず配列上の位置で比較する要素が決まるソーティングネットワークなので、並列計算に利用される。どちらも長さ$2^p$の配列を$\ln (\frac{1}{2})p(p+1)$ステップでソートできる。

奇遇マージソートは、昇順にソートされた2つの配列をマージする。以下の図は配列$a, b$をマージする様子を示す。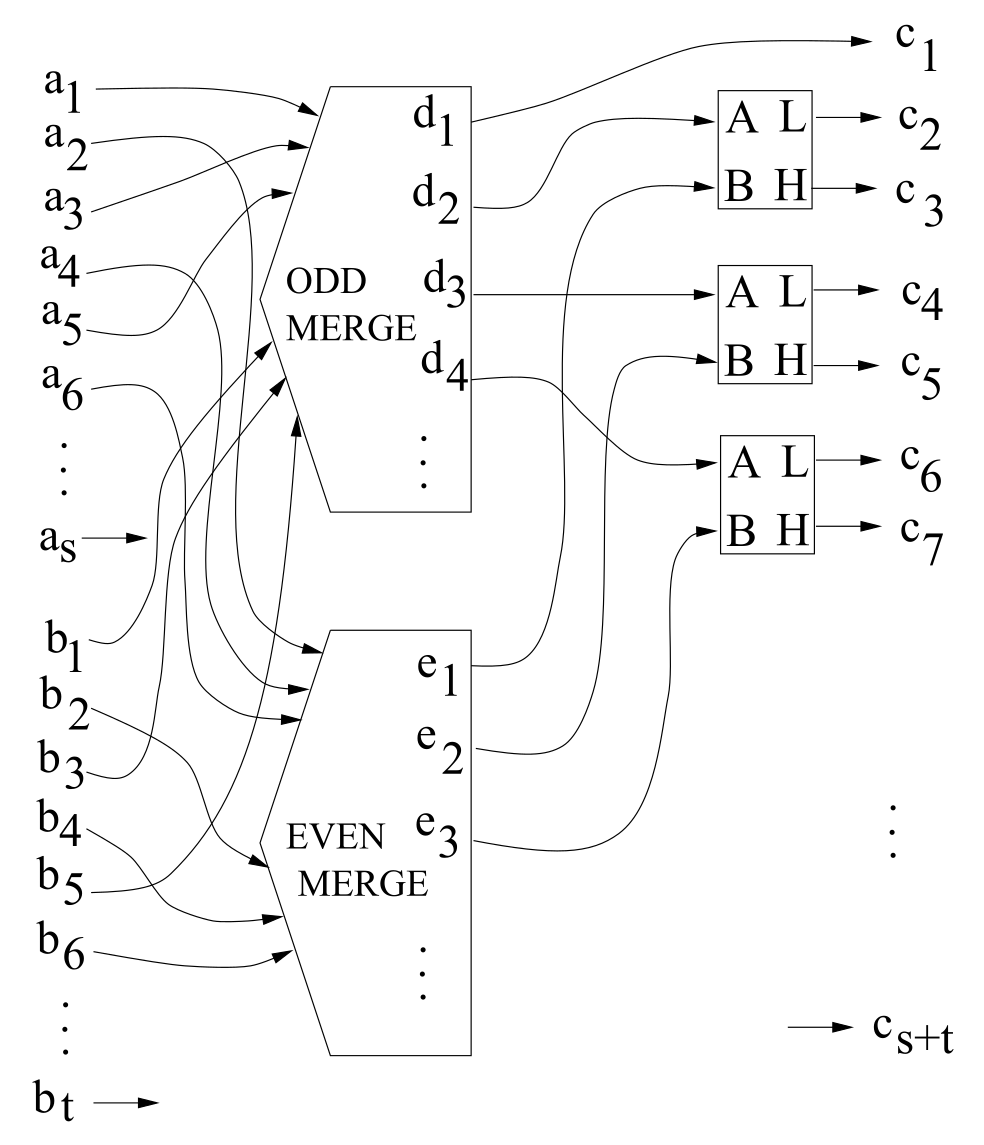図の右にあるA, B, L, Hを囲む枠がノードであり、入力A, Bのうち、大きい方をHに、小さい方をLに出力する。 ODD-MERGEとEVEN-MERGEは$a, b$の奇数または偶数番目の位置にある要素のみからなる配列を再帰的にソートする。 ODD-MERGEの出力の先頭要素は$a, b$の最小値となる。 ODD-MERGEの$i (> 1)$番目の要素とEVEN-MERGEの$i-1$番目の要素の前後関係はノードによって振り分けられる。

昇順の配列と降順の配列を連結してできる配列をバイトニックという。バイトニックソートは、長さ$2n$のバイトニックな配列$a$を受けとり、$a_i$と$a_{n+1}$を比較し、以下の2つのバイトニックな配列を再帰的に生成する。 $$ \begin{align*} \min(a_1, a_{n+1}), \min (a_2, a_{n+2}), \dots , \min (a_n, a_{2n})\\ \max(a_1, a_{n+1}), \max (a_2, a_{n+2}), \dots , \max (a_n, a_{2n}) \end{align*} $$ 任意の$\min(a_i, a_{n+i})$は任意の$\max(a_i, a_{n+i})$以下になるので、2つの配列にそれぞれバイトニックソートを適用した後、連結すればソートされた長さ$2n$の配列になる。以下の図はバイトニックソートの様子を示す。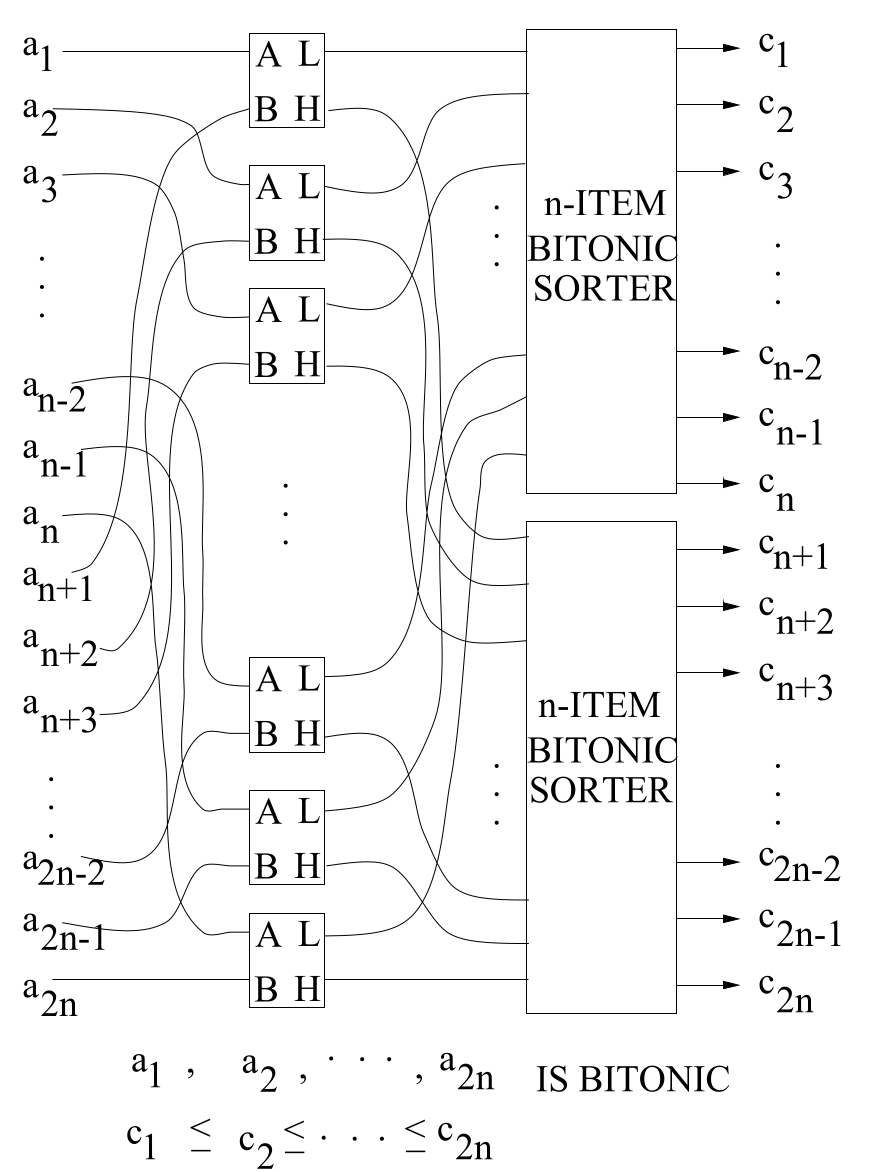 bitonic

図は論文より引用しました。