Wait-Free Synchronization
November 27, 2021あるデータ構造がwait-freeであり、データ構造への操作が有限回のステップで完了するのであれば、ほかの並行プロセスの処理速度によらず、任意のプロセスによるその操作は必ず完了する。 表題のsynchronizationは、wait-freeであるデータ構造で別のwait-freeなデータ構造を実装することを意味する。 実装可能かを定義するためにコンセンサス数を導入する。 あるデータ構造のコンセンサス数は、単純な含意形成問題を解くときに参加できるプロセス数の最大値である。 たとえば、read / writeレジスタのコンセンサス数は1, test & swapは2, compare & swapは無限である。 プロセス数を定義した上で、あるコンセンサス数のデータ構造を、それより小さいコンセンサス数のデータ構造では実装できないことを示した。
あるコンセンサス数のデータ構造でより大きなコンセンサス数のデータ構造を実装できないことを示すために、プロセスやデータ構造をI/O オートマタとみなす。
\(n\)個のプロセス\(P\)と\(m\)個のデータ構造\(A\)として、並行システムを\(\{P_1, \dots , P_n;A_1, \dots , A_m\}\)とおく。
このとき、\(A\)もまた並行システムとみなすことができ、\(F\)を\(P\)から呼ばれるプロシージャ、\(R\)を\(A\)を実装するデータ構造とすると、\(\{F_1, \dots , F_n ; R\}\)とあらわせる。
以下にこの再帰的な様子を図示する。
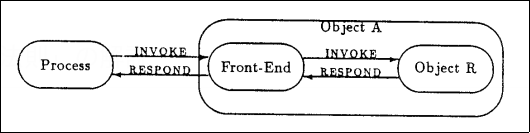
コンセンサス数\(n\)のデータ構造\(X\)と\(m(< n) \)の\(Y\)があり、\(m\)より多数のプロセスが参加するシステムにおいて、\(Y\)による\(X\)の実装がないことを背理法でしめす。 \(k> m\), \(W\)をread/write レジスタ、\(\{F_1, \dots , F_k;W, X\}\)を含意プロトコルでwait-freeであるとする。 \(\{F’_1, \dots , F’_k;Y\}\)が\(X\)の実装とすると、I/Oオートマタの合成の結合性より\(\{F_1, \dots , F_n;W, \{F’_1, \dots , F’_n; Y\}\}\)はwait-freeになる。 これは、合成の結合性から\(\{F_1\cdot F’_1, \dots , F_n \cdot F’_n;W, Y\}\)に等しい。 ところが、これは含意プロトコルであるため、\(Y\)のコンセンサス数が\(m\)であることに反し矛盾する。
論文をこちらからダウンロードできます。 画像は論文から引用されています。